백준 2887번 행성 터널 문제 (Python)
백준 2887번 행성 터널 문제를 Python를 사용하여 해결해 보도록 하겠습니다.
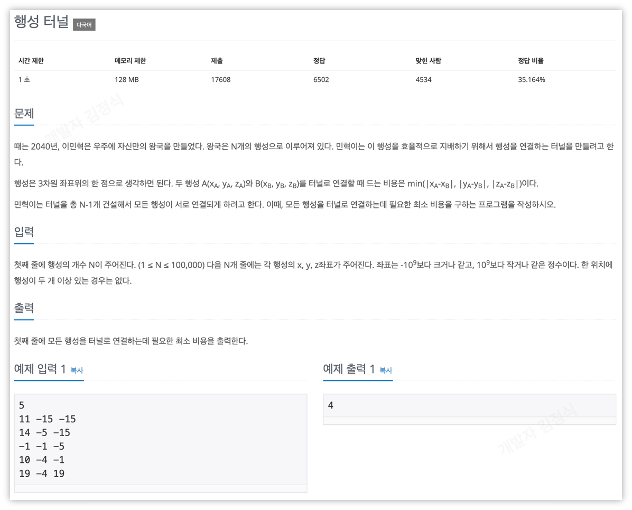
문제
때는 2040년, 이민혁은 우주에 자신만의 왕국을 만들었다. 왕국은 N개의 행성으로 이루어져 있다. 민혁이는 이 행성을 효율적으로 지배하기 위해서 행성을 연결하는 터널을 만들려고 한다.
행성은 3차원 좌표위의 한 점으로 생각하면 된다. 두 행성 A(xA, yA, zA)와 B(xB, yB, zB)를 터널로 연결할 때 드는 비용은 min(|xA-xB|, |yA-yB|, |zA-zB|)이다.
민혁이는 터널을 총 N-1개 건설해서 모든 행성이 서로 연결되게 하려고 한다. 이때, 모든 행성을 터널로 연결하는데 필요한 최소 비용을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 행성의 개수 N이 주어진다. (1 ≤ N ≤ 100,000) 다음 N개 줄에는 각 행성의 x, y, z좌표가 주어진다. 좌표는 -109보다 크거나 같고, 109보다 작거나 같은 정수이다. 한 위치에 행성이 두 개 이상 있는 경우는 없다.
출력
첫째 줄에 모든 행성을 터널로 연결하는데 필요한 최소 비용을 출력한다.
작성한 답
코드
메모리 초과로 실패한 기존 방식
import sys
def find_parent(planet):
if parent_table[planet] == planet:
return planet
else:
parent_table[planet] = find_parent(parent_table[planet])
return parent_table[planet]
def union_parent(planet1, planet2):
parent1 = find_parent(planet1)
parent2 = find_parent(planet2)
parent_table[parent2] = parent1
if __name__ == "__main__":
result = 0
N = int(sys.stdin.readline())
planet_location_list = []
for i in range(N):
x, y, z = map(int, sys.stdin.readline().split())
planet_location_list.append([x, y, z])
edge_between_planet_list = []
for planet1 in range(N - 1):
for planet2 in range(planet1 + 1, N):
x = abs(planet_location_list[planet1][0] - planet_location_list[planet2][0])
y = abs(planet_location_list[planet1][1] - planet_location_list[planet2][1])
z = abs(planet_location_list[planet1][2] - planet_location_list[planet2][2])
edge_between_planet_list.append([planet1, planet2, min(x, y, z)])
edge_between_planet_list.sort(key=lambda v: v[2])
parent_table = [i for i in range(N)]
for planet1, planet2, distance in edge_between_planet_list:
if find_parent(planet1) != find_parent(planet2):
result += distance
union_parent(planet1, planet2)
print(result)
성공한 방식
import sys
def find_parent(planet):
if parent_table[planet] == planet:
return planet
else:
parent_table[planet] = find_parent(parent_table[planet])
return parent_table[planet]
def union_parent(planet1, planet2):
parent1 = find_parent(planet1)
parent2 = find_parent(planet2)
parent_table[parent2] = parent1
if __name__ == "__main__":
result = 0
N = int(sys.stdin.readline())
planet_location_list = []
for i in range(N):
x, y, z = map(int, sys.stdin.readline().split())
planet_location_list.append([x, y, z, i])
edge_between_planet_list = []
for x_y_z in range(3):
planet_location_list.sort(key=lambda v: v[x_y_z])
before_location = planet_location_list[0][3]
for i in range(1, N):
cur_location = planet_location_list[i][3]
edge_between_planet_list.append([before_location, cur_location, abs(planet_location_list[i][x_y_z] - planet_location_list[i - 1][x_y_z])])
before_location = cur_location
edge_between_planet_list.sort(key=lambda v: v[2])
parent_table = [i for i in range(N)]
for planet1, planet2, distance in edge_between_planet_list:
if find_parent(planet1) != find_parent(planet2):
result += distance
union_parent(planet1, planet2)
print(result)
설명
먼저 첫째 줄에 주어지는 행성의 개수 N 만큼 반복하여 각 행성들의 x, y, z 좌표와 각 행성들을 번호로 구분하기 위해 반복문의 index를 사용해 같이 넣어줍니다.
이제 여기서부터가 중요한 부분인데,
다음으로 좌표 기준이 x, y, z 로 3개이므로 3번의 반복문을 돌면서 각 좌표 기준 별로 오름차순으로 정렬을 합니다. 그리고 정렬된 순서로 근접한 행성들끼리의 같은 좌표 기준에서 거리를 행성 번호와 함께 간선 배열에 집어 넣습니다.
이렇게 해야하는 이유는 기존에 실패한 방식에서는 존재할 수 있는 모든 간선을 넣는 방식이었는데 이렇게 하면 코드만 보아도 아시겠지만 O(N^2)가 되기 때문에 메모리 초과가 나오게 됩니다. 어차피 문제는 모든 행성이 서로 연결되기만 하면 되고 연결할 때 최소 비용만을 구하면 되기 때문에 선택되지도 않을 굉장히 먼 거리의 모든 경우의 수를 다 담을 필요가 없습니다. 실패한 방식을 사용한다면 예시는 5개지만 그 수가 늘어나면 엄청나게 커지게 됩니다. 하지만 수정한 성공한 방식으로 하게된다면 O(3N)으로 가능해집니다!
조금 더 자세히 설명하자면 만약 x 좌표를 기준으로 정렬을 햇을 때 2번 행성과 가장 가까이에 있는 행성은 3번 행성이라는 것을 곧바로 알 수 있습니다. 그렇다면 해당 x좌표 기준에서 2번 행성은 0번 행성, 1번 행성, 4번 행성과의 거리를 알 필요가 없는 것입니다. 그렇기 때문에 해당 간선을 비교 대상으로 포함시키지 않아도 되게 됩니다.
이 과정을 거쳐 간선들을 모은 뒤에는 최소 신장 트리를 찾는 크루스칼 알고리즘을 사용하여 문제를 해결할 수 있습니다.
크루스칼 알고리즘에 대해서는 추후에 다른 글에서 자세히 작성할 수 있도록 하겠습니다.
도움이 되셨다면 공감, 댓글 부탁드립니다!
궁금하신 점이나 요청사항은 언제든지 말씀해주세요!
피드백도 언제나 환영입니다!
감사합니다.
'Developer > Algorithm' 카테고리의 다른 글
| 프로그래머스 코딩테스트 연습 Level 2 - 짝지어 제거하기 (JavaScript) (0) | 2022.10.18 |
|---|---|
| 프로그래머스 코딩테스트 연습 Level 2 - 영어 끝말잇기 (JavaScript) (0) | 2022.10.17 |
| 백준 1517번 버블 소트 문제 (Python) (0) | 2022.10.12 |
| 프로그래머스 Level1 2022 KAKAO TECH INTERNSHIP 문제 - 성격 유형 검사하기 (JavaScript) (2) | 2022.09.30 |
| 프로그래머스 코딩테스트 연습 Level 2 - 괄호 회전하기 (JavaScript) (0) | 2022.08.08 |




댓글